martes, 19 de noviembre de 2019
LA PRENSA HIDRAHULICA
Origen y contexto de las prensas hidráulicas
Autor: Gustavo Vargas Antillon
Hoy en día las prensas son muy habituales, pero hace unos años no se conocían.
Fue en el siglo XVII en Francia el matemático y filósofo Blaise Pascal comenzó una investigación referente al principio mediante el cual la presión aplicada a un líquido contenido en un recipiente se transmite con la misma intensidad en todas direcciones.
Con este principio se pueden obtener fuerzas muy grandes utilizando otras más pequeñas
¿Qué son las prensas hidráulicas?
una prensa hidráulica es un mecanismo que está formado por vasos comunicantes impulsados por pistones de diferente área que, mediante pequeñas fuerzas, permite obtener otras mayores. Los pistones son hidráulicos. Estos hacen funcionar conjuntamente a las prensas hidráulicas por medio de motores
¿para que sirve?
Una prensa hidráulica sirve para multiplicar fuerzas. Nos permite que al aplicar fuerzas pequeñas, obtengamos fuerzas grandes.
Se utiliza tanto para prensar como para levantar objetos pesados. Este sistema es utilizado en los frenos hidráulicos. Para la producción en masa, las prensas son empleadas cada día en mayor número, sustituyendo a otras máquinas.
Existe además la razón adicional de que con una buena operación y calidad de las prensas, se pueden obtener productos de mucha homogeneidad, con diferencias de acabado entre unas y otras piezas.
VENTAJAS
Algunas de las principales ventajas de una prensa hidrahulica son las siguientes:
Fuerza: Una prensa hidráulica puede hacer trabajos en ancho rango según su . Entre ellos son: el embutido profundo, reducción, formado de polímetros, el formado, el estampado, troquelado, el punzonado, el prensado, el ensamble ajustado, el enderezo. También es muy útil en los procesos de: el formado de sinterizado de ruedas abrasivas, la adhesión, el brochado, la calibración de diámetros, la compresión a plástico y a hule (goma, caucho), y los troqueles de transferencia.
Tamaño: Aunque una prensa muy común de 20 toneladas mide 1.7 mts por 0.7 mts por 1.5 mts, una prensa de 200 toneladas solo mide 2.1 mts por 1.2 mts por 2 mts, efectivamente con 10 veces la capacidad pero solo un poco más grande; la prensa más grande desplaza solo 50% más. Como va incrementando la fuerza, se va economizando comparando a las prensas mecánicas.
Seguridad: Las prensas son seguras si se usan en la manera apropiada, pero con los controles a dos manos y los protectores enlazados, es más fácil fabricarlas con más seguridad por el hecho del control completo con el sistema hidráulico.
Desventajas
Algunas desventajas de ellas pueden ser:
-La velocidad: No existe ninguna prensa hidráulica que sea tan rápida como una mecánica. Si es que solo importa que la prensa sea rápida y la alimentación sea corta, es mejor una prensa mecánica.
-Choque después del tiempo inicial en proceso de punzón: Ambas prensas, hidráulicas y mecánicas sufren este problema, pero el sistema hidráulico también requiere un aislador del choque relacionado con la descomprensión. Sin esta protección, tal choque puede dañar las líneas y las conexiones.
-Equipo de alimentación automática: Las prensas hidráulicas requieren otra fuerza externa para alimentar la materia prima. El alimentador requiere su propia fuerza, luego tiene que estar integrado con el sistema de control de la prensa. Sin embargo hoy en día existen nuevos sistemas de alimentación: de rollos, de enganche o de aire.
lunes, 21 de octubre de 2019
PRINCIPIO DE PASCAL
Arquímedes y la Corona del Rey Herón
En el siglo III a.C., el rey Hierón II gobernaba Siracusa[1]. Siendo un rey ostentoso, pidió a un orfebre que le crease una hermosa corona de oro, para lo que le dio un lingote de oro puro. Una vez el orfebre hubo terminado, le entregó al rey su deseada corona. Entonces las dudas comenzaron a asaltarle: La corona pesaba lo mismo que un lingote de oro, pero ¿y si el orfebre había sustituido parte del oro de la corona por plata para engañarle?
Ante la duda, el rey hizo llamar a Arquímedes[2]. Arquímedes era uno de los más famosos sabios y matemáticos de la época, así que Hierón creyó que sería la persona adecuada para abordar su problema.
I. Arquímedes
Arquímedes, desde el primer momento, supo que tenía que calcular la densidad de la corona para averiguar así si se trataba de oro puro, o sin embargo contenía algo de plata. La corona pesaba lo mismo que un lingote de oro, así sólo le quedaba conocer el volumen, lo más complicado. El rey Hierón II estaba contento con la corona, y no quería fundirla si no había evidencia de que el orfebre le había engañado, por lo que Arquímedes no podía moldearlo de forma que facilitara el cálculo de su volumen.
Un día, mientras tomaba un baño en una tina, Arquímedes se percató de que el agua subía cuando él se sumergía. En seguida comenzó a asociar conceptos: él al sumergirse estaba desplazando una cantidad de agua que equivaldría a su volumen. Consecuentemente, si sumergía la corona del rey en agua, y medía la cantidad de agua desplazado, podría conocer su volumen.
II. ¡Eureka!
Sin ni siquiera pensar en vestirse, Arquímedes salió corriendo desnudo por las calles emocionado por su descubrimiento, y sin parar de gritar ¡Eureka! ¡Eureka!, lo que traducido al español significa ¡Lo he encontrado!. Sabiendo el volumen y el peso, Arquímedes podría determinar la densidad del material que componía la corona. Si esta densidad era menor que la del oro, se habrían añadido materiales de peor calidad (menos densos que el oro), por lo que el orfebre habría intentado engañar al rey.
Así tomó una pieza de plata del mismo peso que la corona, y otra de oro del mismo peso que la corona. Llenó una vasija de agua hasta el tope, introdujo la pieza de plata y midió la cantidad de agua derramada. Después hizo lo mismo con la pieza de oro. De este modo, determinó qué volumen equivalía a la plata y qué volumen equivalía el oro.
Repitió la misma operación, pero esta vez con la corona hecha por el orfebre. El volumen de agua que desplazó la corona se situó entre medias del volumen de la plata y del oro. Ajustó los cálculos y determinó de forma exacta la cantidad de plata y oro que tenía la corona, demostrando así ante el rey Hierón II que el orfebre le había intentado engañar.
PRINCIPIO DE PASCAL
-PRENSA HIDRAHULICA:
El Principio de Pascal dice que una presión aplicada en cualquier punto de una masa liquida se transmitirá a todas las direcciones posibles. Esto trae consecuencias positivas en cuanto a sus aplicaciones.
Las prensas hidráulicas son dispositivos que constan de dos émbolos. En uno (el menor), se aplica una fuerza determinada y el otro (el mayor) recibe esa fuerza multiplicada. Esto sirve para elevar cuerpos de elevado peso aplicando fuerzas menores. Como el caso de los elevadores de autos o el sillón del odontólogo. Generalmente vistos de arriba tienen forma circular como los que veremos aquí.
La presión por concepto es igual a la fuerza aplicada dividida por la superficie sobre la que actúa la fuerza.
P = F / S
Según Pascal, la presión se transmite en todas las direcciones del fluido. Por lo tanto si aplicamos este concepto en la prensa hidráulica la presión sobre el émbolo menor deberá ser igual a la presión que se recibe en el émbolo mayor.
Por lo tanto si P1 es igual a P2
F1/S1 = F2/S2
Las superficies obviamente son diferentes entre ambos émbolos. Esto explica que las fuerzas también deberán ser diferentes para que los cocientes sean iguales. Si S2 es mayor que S1 F2también será mayor que F1. Aquí radica la ventaja para elevar pesos mayores aplicando una fuerza menor.
Ejemplos:
Calcula la fuerza necesaria que habrá que aplicar a un émbolo chico para elevar un cuerpo que pesa 400 Kgf apoyado en el émbolo mayor. Los radios son respectivamente 6 cm y 24 cm.
Datos:
F1 = ? r1 = 6 cm
F2 = 400 Kgf r2 = 24 cm
La superficie de un círculo responde a la formula: S = p . r 2
Por lo tanto con los radios tenemos las fórmulas de ambas superficies de los émbolos
S1 = p . r1 2 S2 = p . r2 2
Aplicamos la relación de Pascal:
F1/S1 = F2/S2
F1/p . r1 2 = F2/p . r2 2
Ambos p se pueden cancelar por ser del mismo valor y estar en miembros distintos como denominador.
F1/ r1 2 = F2/ r2 2
Podemos despejar F1:
F1 = (F2/ r2 2) . r1 2
F1 = [400 Kgf / (24 cm)2] . (6 cm)2
F1 = [400 Kgf / 576 cm2] . 36 cm2
Los cm2 se cancelan quedando como unidad de fuerza el Kgf.
F1 = 25 Kgf
Como se observa, para elevar a 400 Kgf solo se necesitan 25 Kgf.
https://quimicayalgomas.com/fisica/teorema-de-pascal-prensa-hidraulica/
En el siglo III a.C., el rey Hierón II gobernaba Siracusa[1]. Siendo un rey ostentoso, pidió a un orfebre que le crease una hermosa corona de oro, para lo que le dio un lingote de oro puro. Una vez el orfebre hubo terminado, le entregó al rey su deseada corona. Entonces las dudas comenzaron a asaltarle: La corona pesaba lo mismo que un lingote de oro, pero ¿y si el orfebre había sustituido parte del oro de la corona por plata para engañarle?
Ante la duda, el rey hizo llamar a Arquímedes[2]. Arquímedes era uno de los más famosos sabios y matemáticos de la época, así que Hierón creyó que sería la persona adecuada para abordar su problema.
I. Arquímedes
Arquímedes, desde el primer momento, supo que tenía que calcular la densidad de la corona para averiguar así si se trataba de oro puro, o sin embargo contenía algo de plata. La corona pesaba lo mismo que un lingote de oro, así sólo le quedaba conocer el volumen, lo más complicado. El rey Hierón II estaba contento con la corona, y no quería fundirla si no había evidencia de que el orfebre le había engañado, por lo que Arquímedes no podía moldearlo de forma que facilitara el cálculo de su volumen.
Un día, mientras tomaba un baño en una tina, Arquímedes se percató de que el agua subía cuando él se sumergía. En seguida comenzó a asociar conceptos: él al sumergirse estaba desplazando una cantidad de agua que equivaldría a su volumen. Consecuentemente, si sumergía la corona del rey en agua, y medía la cantidad de agua desplazado, podría conocer su volumen.
II. ¡Eureka!
Sin ni siquiera pensar en vestirse, Arquímedes salió corriendo desnudo por las calles emocionado por su descubrimiento, y sin parar de gritar ¡Eureka! ¡Eureka!, lo que traducido al español significa ¡Lo he encontrado!. Sabiendo el volumen y el peso, Arquímedes podría determinar la densidad del material que componía la corona. Si esta densidad era menor que la del oro, se habrían añadido materiales de peor calidad (menos densos que el oro), por lo que el orfebre habría intentado engañar al rey.
Así tomó una pieza de plata del mismo peso que la corona, y otra de oro del mismo peso que la corona. Llenó una vasija de agua hasta el tope, introdujo la pieza de plata y midió la cantidad de agua derramada. Después hizo lo mismo con la pieza de oro. De este modo, determinó qué volumen equivalía a la plata y qué volumen equivalía el oro.
Repitió la misma operación, pero esta vez con la corona hecha por el orfebre. El volumen de agua que desplazó la corona se situó entre medias del volumen de la plata y del oro. Ajustó los cálculos y determinó de forma exacta la cantidad de plata y oro que tenía la corona, demostrando así ante el rey Hierón II que el orfebre le había intentado engañar.
PRINCIPIO DE PASCAL
-PRENSA HIDRAHULICA:
El Principio de Pascal dice que una presión aplicada en cualquier punto de una masa liquida se transmitirá a todas las direcciones posibles. Esto trae consecuencias positivas en cuanto a sus aplicaciones.
Las prensas hidráulicas son dispositivos que constan de dos émbolos. En uno (el menor), se aplica una fuerza determinada y el otro (el mayor) recibe esa fuerza multiplicada. Esto sirve para elevar cuerpos de elevado peso aplicando fuerzas menores. Como el caso de los elevadores de autos o el sillón del odontólogo. Generalmente vistos de arriba tienen forma circular como los que veremos aquí.
La presión por concepto es igual a la fuerza aplicada dividida por la superficie sobre la que actúa la fuerza.
P = F / S
Según Pascal, la presión se transmite en todas las direcciones del fluido. Por lo tanto si aplicamos este concepto en la prensa hidráulica la presión sobre el émbolo menor deberá ser igual a la presión que se recibe en el émbolo mayor.
Por lo tanto si P1 es igual a P2
F1/S1 = F2/S2
Las superficies obviamente son diferentes entre ambos émbolos. Esto explica que las fuerzas también deberán ser diferentes para que los cocientes sean iguales. Si S2 es mayor que S1 F2también será mayor que F1. Aquí radica la ventaja para elevar pesos mayores aplicando una fuerza menor.
Ejemplos:
Calcula la fuerza necesaria que habrá que aplicar a un émbolo chico para elevar un cuerpo que pesa 400 Kgf apoyado en el émbolo mayor. Los radios son respectivamente 6 cm y 24 cm.
Datos:
F1 = ? r1 = 6 cm
F2 = 400 Kgf r2 = 24 cm
La superficie de un círculo responde a la formula: S = p . r 2
Por lo tanto con los radios tenemos las fórmulas de ambas superficies de los émbolos
S1 = p . r1 2 S2 = p . r2 2
Aplicamos la relación de Pascal:
F1/S1 = F2/S2
F1/p . r1 2 = F2/p . r2 2
Ambos p se pueden cancelar por ser del mismo valor y estar en miembros distintos como denominador.
F1/ r1 2 = F2/ r2 2
Podemos despejar F1:
F1 = (F2/ r2 2) . r1 2
F1 = [400 Kgf / (24 cm)2] . (6 cm)2
F1 = [400 Kgf / 576 cm2] . 36 cm2
Los cm2 se cancelan quedando como unidad de fuerza el Kgf.
F1 = 25 Kgf
Como se observa, para elevar a 400 Kgf solo se necesitan 25 Kgf.
https://quimicayalgomas.com/fisica/teorema-de-pascal-prensa-hidraulica/
https://www.cienciasatlantico.blogsek.es/2013/02/19/fuerza-de-empuje-principio-de-arquimedes-peso-aparente/
PRINCIPIO DE ARQUÍMEDES
«Todo cuerpo sumergido en un fluido (líquido o gas). Experimenta una fuerza vertical y hacia arriba – fuerza de empuje (E)- cuyo módulo es igual al peso del volumen de fluido que desaloja.
E = V sumergido · d líquido · g
Donde:
E, empuje (N)
V sumergido, Volumen del cuerpo sumergido (m^3)
d líquido, Densidad del líquido (kg/m^3) RECUERDA: LA DENSIDAD DEL AGUA PURA ES 1000 kg/ m^3
g, Gravedad (9.8 m/ s^2)
¿QUÉ SITUACIONES NOS PODEMOS ENCONTRAR CUANDO UN CUERPO ES INTRODUCIDO EN UN LÍQUIDO?
1. El peso del objeto completamente sumergido es mayor que el empuje. En este caso, la resultante es una fuerza vertical hacia abajo que hace que el cuerpo se hunda.
2. El peso y el empuje son iguales en módulo. Entonces, la resultante es nula. El cuerpo se encontrará en equilibrio y se mantendrá en la posición en que se ha colocado.
3. El peso del objeto sumergido es menor que el empuje. La resultante es una fuerza vertical hacia arriba que hace emerger el cuerpo. El equilibrio se alcanza cuando el objeto se mantiene parcialmente sumergido, lo suficiente para que sean iguales su peso y el empuje correspondiente.
¿QUÉ ES EL PESO APARENTE?
Cuando un cuerpo está totalmente sumergido en un fluido, este experimenta un empuje que tiene sentido opuesto al peso del objeto. La fuerza resultante por lo tante es inferior al peso que tendría el cuerpo en el aire, a este peso (en el agua) se le denomina peso aparente.
Podrás encontrar un ejercicio modelo sobre el peso aparente en el siguiente enlace
PROPUESTA DE ACTIVIDAD EXPERIMENTAL
PRACTICA: APLICACION DEL PRINCIPIO DE ARQUIMIDES EN LIQUIDOS
OBJETIVOS
1º) Determinación de la densidad de un cuerpo
2º) Determinación de la densidad de un líquido
MATERIAL A UTILIZAR
- - Varilla con soporte
- - Pinza con gancho
- - Dinamómetro
- - Pesas
- - Probeta graduada de 250 ml
ELABORACIÓN DEL EXPERIMENTO
Experiencia 1.-. En primer lugar, calculamos el peso real del cuerpo, colgándolo del dinamómetro, el cual nos indica directamente el peso en Newtons. A continuación, Introducimos agua en la probeta hasta un cierto volumen, de tal manera que el cuerpo quede sumergido en el líquido, con lo cual calculamos el peso aparente en agua, tal como lo indica la lectura en el dinamómetro. Esto nos permite calcular el empuje según la expresión:
E = Preal - Paparente
A continuación, calculamos el volumen del cuerpo, despejándolo de la expresión del principio de Arquímedes:
E = dl.Vc.g
comparándolo con el valor experimental observado al comprobar el incremento del volumen del líquido, que debe ser del mismo orden o similar, debido a los errores de precisión y cálculo.
Por último, calculamos la masa del cuerpo por la expresión : Preal = m.g, y finalmente, ya podemos calcular la densidad del cuerpo:
dc = mc/Vc
ejemplo práctico:
peso real: 1.5 N
peso aparente: 1.3 N
empuje = 0.2 N
volumen inicial del agua en la probeta : 220 ml
volumen final del agua en la probeta : 239 ml
incremento de volumen: 19 ml
El cálculo del volumen por la fórmula Vc= E / dl.g = 2,04.10-5 m3 = 20.4 ml(valor similar)
Por último, calculamos la densidad del cuerpo:
dc = mc/Vc = 0.153 / 2,04.10-5 = 7503 Kg/m3
Experiencia 2.- Para calcular la densidad de un líquido en el que se sumerge un cuerpo, es necesario conocer el volumen del cuerpo, lo que calculamos por la expresión: Vc=mc/dc (la densidad del cuerpo es un dato que nos deben dar, y la masa del cuerpo la sacamos del peso real: Pr = mc.g)
Una vez calculado el peso real utilizando el dinamómetro, hallamos el peso aparente al introducir el cuerpo en el líquido de densidad desconocida. Esto nos permite calcular el empuje:
E= Pr – Pap
El siguiente paso consistirá en calcular la densidad del líquido a estudio, despejándola de la expresión:
E = dl Vc g
Con lo cual, tendremos:
dl = E / Vc g
ejemplo práctico :
peso real: 1.5 N
peso aparente: 1 N
empuje = 0.5 N
Vc = 2,04.10-5 m3
Con estos datos, la densidad sería : dl = 0.5 / 2,04.10-5 . 9.8 = 2.500 Kg/m3
URL'S:
https://quimicayalgomas.com/fisica/teorema-de-pascal-prensa-hidraulica/
https://www.cienciasatlantico.blogsek.es/2013/02/19/fuerza-de-empuje-principio-de-arquimedes-peso-aparente/
https://www.google.com.mx/search?sxsrf=ACYBGNTXN7BEr039Bgi6O4TS7CN2t-OEpg%3A1571664819688&ei=s7OtXdXJKeLY9APSyrmABQ&q=+actividad+experimental+para+el+c%C3%A1lculo+de+la+Fuerza+de+Empuje.&oq=+actividad+experimental+para+el+c%C3%A1lculo+de+la+Fuerza+de+Empuje.&gs_l=psy-ab.3...9037.13516..13909...1.2..1.127.462.0j4......0....1j2..gws-wiz.....10..0i71j0j0i7i30j0i131j35i362i39.3Zd5WWztNWo&ved=0ahUKEwiV76Hau63lAhViLH0KHVJlDlAQ4dUDCAs&uact=5
miércoles, 16 de octubre de 2019
PRESIÓN DE FLUIDOS
Esta presión, llamada presión hidrostática, provoca, en fluidos en reposo, una fuerza perpendicular a las paredes del recipiente o a la superficie del objeto sumergido sin importar la orientación que adopten las caras. ... es la altura del fluido (en metros).
Un sistema de transmisión de energía que usa la fuerza del flujo de líquidos y gases para transmitir energía. Los sistemas de fluido incluyen sistemas hidráulicos y sistemas neumáticos.
Medición de la presión de un fluido
La medición y el control de presión son las variables de proceso más usadas en los más distintos sectores de la industria de control de procesos. Además, a través de la presión se puede inferir fácilmente una serie de otras variables, tales como, nivel, volumen, flujo y densidad. En este artículo comentaremos las principales características de las tecnologías más importantes utilizadas en sensores de presión, y también algunos detalles sobre instalaciones, mercado y tendencias de los transmisores de presión.
La presión atmosférica corresponde a la presión que ejerce el aire alrededor nuestro y varía dependiendo de las condiciones atmosféricas y de la altitud a la que nos encontremos. A nivel del mar, el valor de la presión atmosférica se considera constante e igual a 101.325 kPa. En realidad es un promedio y se denomina “presión atmosférica estándar”. Este valor nos sirve como referencia para el cálculo de la presión.
1 atm = 101.325 kPa = 760 mmHg = 10.34 mH2O = 14.7 lb/pul2 = 2116 lb/pie2
En el contexto de la Mecánica de fluidos, el término “vacío” se refiere a un espacio en el que la presión es menor que la presión atmosférica. El vacío se cuantifica en términos de cuál es su diferencia con respecto a la presión atmosférica. Si tenemos un recipiente cerrado dentro del cual la presión es de 90 kPa, esto corresponderá a una presión de vacío de (101.325-90) kPa.
Consideramos dos tipos de presión, la presión absoluta y la presión relativa.
- Presión absoluta -> se mide con respecto al cero absoluto de presión, el cual corresponde a la presión más baja posible en un vacío perfecto como su base.
- Presión relativa -> se mide con respecto a la presión atmosférica.
Por ejemplo, si un fluido tiene una presión de 5.5 kPa, con respecto a la presión atmosférica, esa será su presión relativa, mientras que su presión absoluta es (101.325 + 5.500), esto es, 106.825 kPa.
¿Con qué se mide la presión?
Para medir la presión se pueden utilizar distintos dispositivos.
Barómetros -> es un aparato que se usa para medir la presión atmosférica. Consiste de un tubo de vidrio cerrado en un extremo y lleno de mercurio, cuya longitud es superior a 762 mm y el cual tiene una escala reglada en mm para poder medir en ella la altura alcanzada por el mercurio dentro del tubo. El tubo se coloca verticalmente con el extremo abierto sumergido en una cubeta llena de mercurio, la cual está abierta y en contacto con la atmósfera. En el espacio libre dentro del tubo y por encima del mercurio hay vapor de mercurio a una presión correspondiente a la presion de vapor del mercurio.





LEY DE PASCAL PARA EL SENO DE UN FLUIDO


se resume en la frase: la presión ejercida por un fluido incompresible y en equilibrio dentro de un recipiente de paredes indeformables se transmite con igual intensidad en todas las direcciones y en todos los puntos del fluido.
El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma velocidad y por lo tanto con la misma presión.
Presión Absoluta


Es la presión de un fluido medido con referencia al vacío perfecto o cero absoluto. La presión absoluta es cero únicamente cuando no existe choque entre las moléculas lo que indica que la proporción de moléculas en estado gaseoso o la velocidad molecular es muy pequeña. Ester termino se creo debido a que la presión atmosférica varia con la altitud y muchas veces los diseños se hacen en otros países a diferentes altitudes sobre el nivel del mar por lo que un termino absoluto unifica criterios.

Presión Atmosférica
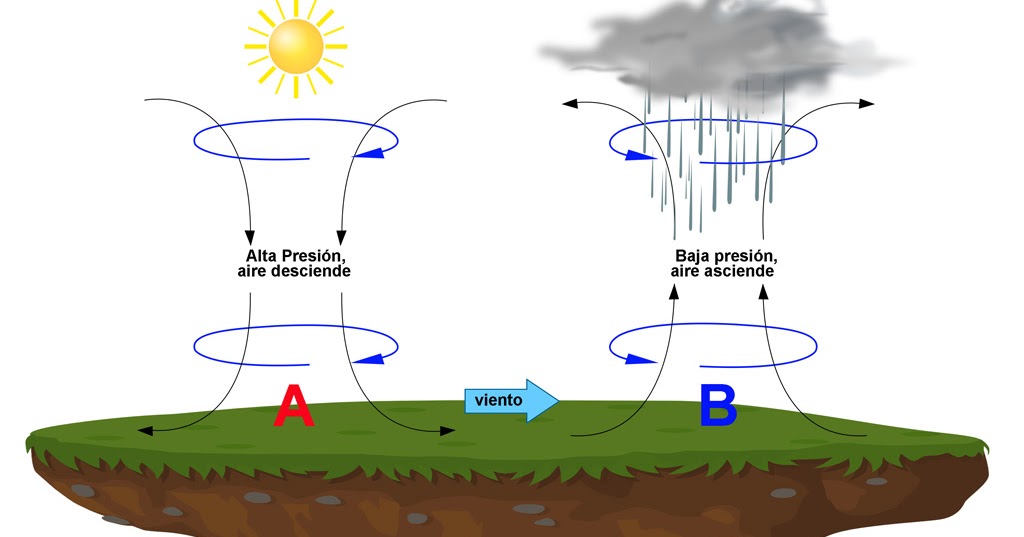

El hecho de estar rodeados por una masa gaseosa (aire), y al tener este aire un peso actuando sobre la tierra, quiere decir que estamos sometidos a una presión (atmosférica), la presión ejercida por la atmósfera de la tierra, tal como se mide normalmente por medio del barómetro (presión barométrica). Al nivel del mar o a las alturas próximas a este, el valor de la presión es cercano a 14.7 lb/plg2 (101,35Kpa), ,disminuyendo estos valores con la altitud.
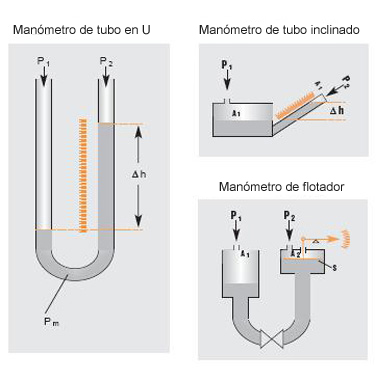
Presión Manométrica
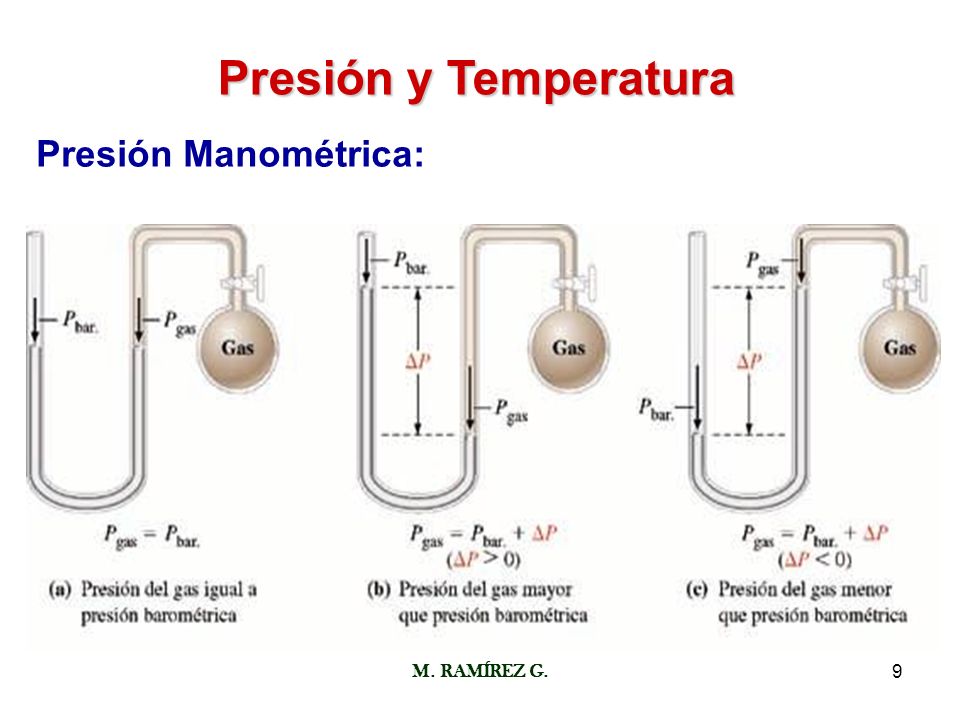

Son normalmente las presiones superiores a la atmosférica, que se mide por medio de un elemento que se define la diferencia entre la presión que es desconocida y la presión atmosférica que existe, si el valor absoluto de la presión es constante y la presión atmosférica aumenta, la presión manométrica disminuye; esta diferencia generalmente es pequeña mientras que en las mediciones de presiones superiores, dicha diferencia es insignificante, es evidente que el valor absoluto de la presión puede abstenerse adicionando el valor real de la presión atmosférica a la lectura del manómetro.
La presión puede obtenerse adicionando el valor real de la presión atmosférica a la lectura del manómetro.
Presión Absoluta = Presión Manométrica + Presión Atmosférica.
Suscribirse a:
Comentarios (Atom)


